เรื่องเล่าจากภาพวาด: โมนาลิซากับคณิตศาสตร์

เรื่องเล่าจากภาพวาด: โมนาลิซากับคณิตศาสตร์

994
ที่มา Youtube

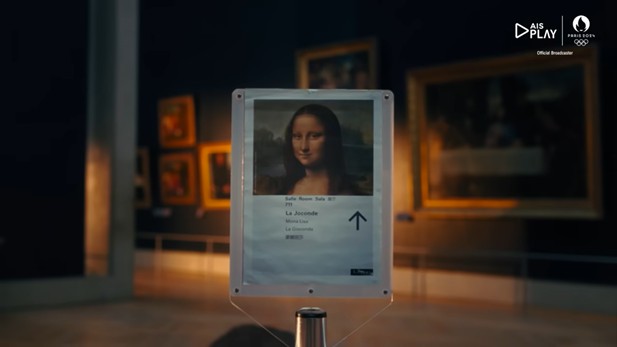
ช่วงเวลาของพิธีเปิดโอลิมปิก 2024 ที่นครปารีส  ท่านอาจจะผ่านตากับผลงานอมตะ “โมนาลิซา” ซึ่งวาดโดย เลโอนาโด ดา วินชี (Leonardo da Vinci) จิตรกรเอก นักวิทยาศาสตร์ และนักประดิษฐ์ ชาวอิตาลี ที่มีชีวิตอยู่ระหว่างปี ค.ศ. 1452-1519 โดยภาพนี้เป็นหนึ่งในภาพวาดที่มีชื่อเสียงมากที่สุดในโลก ความน่าสนใจของภาพมากจากเทคนิคที่ ดา วินชี ใช้ในการวาดภาพนี้ ได้แก่ เทคนิค Atmospheric Perspective ที่วาดภาพฉากด้านหลังแบบเลือนซึ่งเป็นการสร้างความลึกตื้นให้กับภาพ และเทคนิค Sfumato หรือ สฟูมาโต ที่เกลี่ยสี (gradation of color) บริเวณเส้นขอบของบุคคลหรือวัตถุทำให้มีความละมุนมากขึ้น ภาพที่ได้ออกมาดูใกล้เคียงและสมจริงเหมือนที่สายตามนุษย์มองเห็น นอกเหนือจากเทคนิคที่เหนือชั้นแล้ว การที่ภาพโมนาลิซาเคยถูกขโมยหายไปจากพิพิธภัณฑ์ลูฟวร์ในระยะเวลาหนึ่งยังเป็นส่วนสร้างชื่อให้กับภาพนี้อีกด้วย ในปัจจุบันภาพโมนาลิซาจัดแสดงที่ห้อง Salle des États พิพิธภัณฑ์ลูฟวร์ นครปารีส สาธารณรัฐฝรั่งเศส โดยสามารถชมความงามของภาพโมนาลิซา และภาพอื่น ๆ ที่จัดแสดงใน Salle des États ได้ทาง https://www.louvre.fr/louvreplus/video-au-louvre-la-salle-des-etats?autoplay

นอกจากเทคนิคการวาดภาพที่น่าทึ่งของ ดา วินชี แล้ว ท่านรู้หรือไม่ว่าภาพโมนาลิซานี้ ยังพ้องกับข้อมูลด้านคณิตศาสตร์ที่ส่งผลให้ภาพมีความสมดุล สวยงาม และรื่นตาอีกด้วย

ภาพวาดเลโอนาโด ดา วินชี  (ที่มา Wikipedia) 
ภาพโมนาลิซา โดย เลโอนาโด ดา วินชี  (ที่มา Wikipedia)

อัตราส่วนทอง (Golden Ratio) หรือ Phi (Φ)  ที่ทำให้ภาพโมนาลิซาได้สมดุลและสวยงาม เป็นจำนวนอตรรกยะมีค่าประมาณ 1.618 โดยกำหนดจากสมการทางคณิตศาสตร์ที่เมื่อแบ่งเส้นตรงหนึ่งออกเป็นสองส่วน ค่าอัตราส่วนระหว่างทั้งเส้นกับส่วนที่ยาวกว่าจะเท่ากับอัตราส่วนระหว่างส่วนที่ยาวกว่ากับส่วนที่สั้นกว่า ซึ่งสัดส่วนนี้พบได้ในธรรมชาติและในศิลปะต่าง ๆ ซึ่งมีความสมดุล สวยงามและสมบูรณ์

ตัวอย่างเช่น ถ้ามีเส้นตรงหนึ่งเส้นที่แบ่งออกเป็นสองส่วน ได้แก่ ส่วนยาว (a) และส่วนสั้น (b) ถ้าความสัมพันธ์ระหว่างทั้งสองส่วนนี้เป็นไปตามอัตราส่วนทอง ความยาวของส่วนยาว (a) หารด้วยความยาวของส่วนสั้น (b) จะได้ค่าใกล้เคียงกับ 1.618 นอกจากนี้อัตราส่วนทองนี้มีความเชื่อมโยงกับลำดับฟิโบนักชี (Fibonacci Sequence) ซึ่งลำดับฟิโบนักชี คือ ลำดับของจำนวนที่สองพจน์แรกคือ 0 และ 1 ตามลำดับ หลังจากนั้น ทุกพจน์ในลำดับจะเป็นผลรวมของสองพจน์ก่อนหน้า โดยลำดับจะเป็นดังต่อไปนี้ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…  จะเห็นว่าพจน์ที่สามหรือ 1 คือผลจาก 0+1 ส่วนพจน์ที่สี่หรือ 2 คือ 1+1 และพจน์ที่ห้าหรือ 3 คือ 2+1 ซึ่งทั้งหมดที่กล่าวมาคือสองพจน์ก่อนหน้าในลำดับนั่นเอง

ภาพแสดงลำดับฟิโบนักชี

และเมื่อจำนวนในลำดับฟิโบนักชีเพิ่มขึ้นเรื่อย ๆ จะนำไปสู่อัตราส่วนทอง ตัวอย่างเช่น ถ้านำจำนวนในลำดับฟิโบนักชีที่ต่อเนื่องกันมาหารกัน เช่น 21 ÷ 13 หรือ 34 ÷ 21 ค่าที่ได้จะใกล้เคียงกับ 1.618 ซึ่งเป็นอัตราส่วนทองนั่นเอง

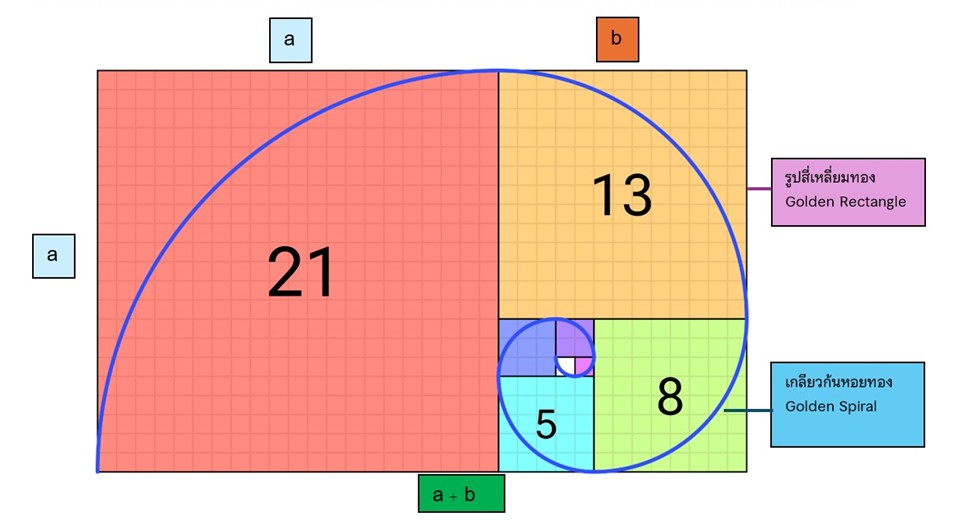
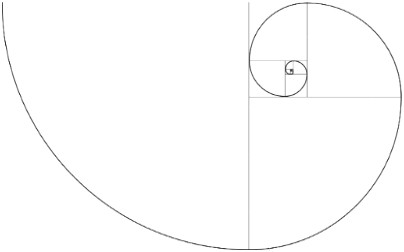
ภาพแสดงเกลียวก้นหอยทอง (Golden Spiral) ที่ประมาณด้วยเกลียวก้นหอยฟิโบนักชี (Fibonacci Spiral) โดย Romain (ที่มา Wikipedia)

จากภาพ a คือ ส่วนยาว = 21 ส่วน b คือ ส่วนสั้น = 13  และ  a  + b คือความยาวรวมส่วนยาวและส่วนสั้น = 34
จะได้ a/b = 21/13 มีค่าใกล้เคียงกับ a+b/b = 34/21 ซึ่งมีค่าประมาณ 1.615 และ 1.619 ตามลำดับ

โดยสำหรับอัตราส่วนทอง ความยาวของส่วนยาว หารด้วย ความยาวของส่วนสั้น = ความยาวรวมส่วนยาวและส่วนสั้น หารด้วย ความยาวของส่วนยาว มีค่าใกล้เคียงกับ 1.618

เมื่อย้อนกลับมาดูที่ภาพโมนาลิซา และนำเกลียวก้นหอยทอง และรูปสี่เหลี่ยมทองไปทาบ จะพบว่าเกลียวก้นหอยทอง ทาบทับอย่างพอดีกับส่วนลำตัวและศีรษะของโมนาลิซา (ภาพกลาง) โดยความยาวของศีรษะและลำตัวของโมนาลิซา มีอัตราส่วนคือ 1:1.618 หรือหากทาบรูปสี่เหลี่ยมทอง ดังเส้นสีเหลือง (ภาพขวา) ก็จะได้อัตราส่วนดังกล่าวเช่นกัน เช่นเดียวกับเส้นประสีขาว ซึ่งแบ่งภาพเป็นสามส่วนทั้งแนวตั้งและแนวนอน จะพบว่ามีอัตราส่วนคือ 1:1.618 และสำหรับอัตราส่วนบริเวณศีรษะ ดังเส้นสีม่วง พบว่าอัตราส่วนระหว่างบริเวณคางถึงจมูกและจมูกถึงศีรษะคือ 1:1.618 นอกจากนี้หากทาบเกลียวก้นหอยทองหรือรูปสี่เหลี่ยมทองบริเวณดวงตาของโมนาลิซาก็จะพบว่ามีอัตราส่วนทองเช่นเดียวกัน ซึ่งอัตราส่วนดังกล่าวทำให้ภาพมีความสมดุล และดึงดูดมาก โดยเฉพาะบริเวณรอยยิ้มและดวงตาของโมนาลิซาที่มีความลึกลับ น่าค้นหา และคล้ายกับว่ากำลังสบตากับผู้ชมภาพตลอดเวลา

ภาพการนำเกลียวก้นหอยทองและรูปสี่เหลี่ยมทองไปทาบกับภาพโมนาลิซา (ซ้าย, ภาพจาก goldenratiocolors และ ขวา, ภาพจากกิจกรรมของ Museum of Science)

สำหรับการประยุกต์ใช้อัตราส่วนทองหรือลำดับฟิโบนักชี ในงานศิลป์นั้น มีตัวอย่างอีกมากมาย เช่น การถ่ายภาพในชีวิตประจำวัน การวางองค์ประกอบภาพโดยอิงอัตราส่วนทองหรือลำดับฟิโบนักชี จะเป็นการเน้นจุดที่ต้องการให้เกิดความสมดุล ได้สัดส่วนและสวยงามต้องตา   

ภาพโดย © Ansel Adams ดัดแปลงโดย photographyhero

จะสังเกตได้ว่าจุดที่ Ansel Adams ต้องการเน้นคือจุดยอดเขาทางด้านขวามือ ซึ่งเมื่อทาบเกลียวก้นหอยทอง จุดเน้นจะอยู่บริเวณปลายก้นหอยพอดี หรืออีกภาพโดย Henri Cartier- Bresson ที่ถ่ายภาพบันไดเวียนและชายขี่จักรยาน จากภาพจะเห็นว่าตัวเส้นเกลียวก้นหอย ค่อย ๆ นำสายตาของผู้มองภาพจากบันไดมายังจุดปลายก้นหอยคือชายขี่จักรยานซึ่งเป็นจุดเน้นของภาพ

ภาพโดย © Henri Cartier- Bresson ดัดแปลงโดย photographyhero

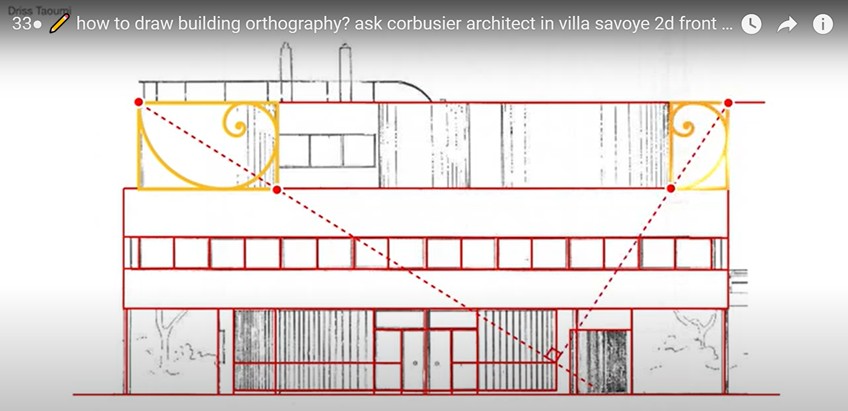
นอกเหนือจากงานภาพถ่ายแล้ว งานด้านการออกแบบสถาปัตยกรรมได้นำอัตราส่วนทองมาประกอบในการออกแบบด้วย เช่น เลอกอร์บูซิเยร์ (Le Corbusier, ค.ศ. 1887 – ค.ศ. 1965) สถาปนิกชื่อก้องโลกที่ผลงานได้รับขึ้นทะเบียนเป็นมรดกโลกที่มีความพิเศษด้านวัฒนธรรมถึง 17 ผลงาน ซึ่งเลอกอร์บูซิเยร์เน้นประโยชน์ใช้สอยเป็นสิ่งที่สำคัญที่สุด และเป็นผู้คิดค้นทฤษฎีทางสถาปัตยกรรม เช่น Le Modulor, ลักษณะทางสถาปัตยกรรม 5 ประการ หรือ DOM-INO system เป็นต้น เลอกอร์บูซิเยร์ออกแบบ Villa Savoye ด้วยทฤษฎีโมดูลอร์  ซึ่งมีสัดส่วนที่ใกล้เคียงกับอัตราส่วนทอง นอกจากนี้การวางแพลนและสัดส่วนของห้องและองค์ประกอบอื่น ๆ เช่น ประตูหรือหน้าต่าง ต่างก็ขึ้นกับอัตราส่วนทองเช่นกัน เพื่อให้เกิดความกลมกลืน ต่อเนื่องและสมดุล  

ภาพเลอกอร์บูซิเยร์
ภาพ Villa Savoye ซึ่งได้รับการขึ้นทะเบียนเป็นมรดกโลกโดยยูเนสโก© FLC / ADAGP / © Jean-Christophe Ballot / Dist.Centre des monuments nationaux (Base Regards)

(ภาพเลอกอร์บูซิเยร์ และ Villa Savoye จาก foundationcorbusier)

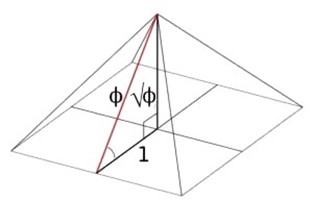
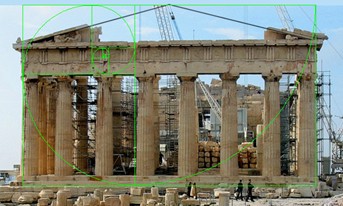
ภาพแสดงอัตราส่วนทอง และเกลียวก้นหอยทอง ในการออกแบบ Villa Savoye ของเลอกอร์บูซิเยร์ (ภาพจาก youtube)

นอกจากสถาปัตยกรรมปัจจุบันแล้ว สถาปัตยกรรมในอดีตต่างก็ออกแบบด้วยแนวคิดที่ใกล้เคียงอัตราส่วนทอง เช่น มหาพีระมิดแห่งกีซา ประเทศอียิปต์พบว่าอัตราส่วนของส่วนสูงเอียงต่อความยาวจากจุดกึ่งกลางของฐานรูปสี่เหลี่ยมมายังแต่ละด้านของพีระมิด จะได้ค่าประมาณ 1.618 หรือ มหาวิหารพาร์เธนอน ที่ประเทศกรีซ พบว่าอัตราส่วนของความกว้างและความยาวของ façade ของมหาวิหารมีค่าใกล้เคียงกับอัตราส่วนทองเช่นกัน

ภาพมหาพีระมิดแห่งกีซา (โดย Simon Berger)
ภาพแสดงสัดส่วนของมหาพีระมิดแห่งกีซา (โดย goldennumber)
ภาพมหาวิหารพาร์เธนอน (โดย goldennumber)

อ้างอิง :

อ้างอิงภาพ :

เฉลย!

ในธรรมชาติ สามารถพบอัตราส่วนทองหรือลำดับฟิโบนักชี ได้ใน

1) การเรียงตัวของเมล็ดทานตะวัน ซึ่งจะเรียงตัวเป็นเกลียว หากนับตามเข็มนาฬิกาจะได้ 21 เกลียว ในขณะที่ถ้านับทวนเข็มนาฬิกาจะได้ 34 เกลียว หรือ นับตามเข็มนาฬิกา 34 เกลียว แต่เมื่อนับทวนเข็มนาฬิกาจะได้ 55 เกลียว ซึ่งอัตราส่วนของจำนวนเกลียวตามเข็มนาฬิกาต่อจำนวนเกลียวทวนเข็มนาฬิกา จะใกล้เคียง 1.618 เสมอ ซึ่งการเรียงเมล็ดในรูปแบบนี้จะเป็นการเรียงตัวที่ได้เมล็ดมากที่สุดเพื่อการขยายพันธุ์ของทานตะวันต่อไป

ภาพการเรียงตัวของเมล็ดดอกทานตะวัน (ภาพโดย mathnasium)

2) เปลือกหอยงวงช้าง จากภาพจะพบว่าเปลือกของหอยงวงช้างมีรูปแบบที่ใกล้เคียงกับเกลียวก้นหอยทองเป็นอย่างมาก

ภาพหอยงวงช้างในพิพิธภัณฑ์สัตว์น้ำ (ภาพโดย sandrine RONGÈRE)
ภาพเกลียวก้นหอยทอง (ภาพโดย Wikipedia)

3) กลีบดอกไม้ กลีบดอกไม้มักจะเป็นจำนวนเหล่านี้ 3, 5, 8, 13, 21, 34, หรือ 55 ซึ่งคือพจน์ของลำดับฟิโบนักชี นั่นเอง

ภาพแสดงจำนวนกลีบดอกไม้ (ภาพโดย letstalkscience)

ส่งข้อความถึงเรา