
สมการชเรอดิงเงอร์ คือสมการที่เป็นหัวใจสำคัญของ กลศาสตร์ควอนตัม (Quantum Mechanics) คิดค้นโดย แอร์วิน ชเรอดิงเงอร์ (Erwin Schrödinger) นักฟิสิกส์ชาวออสเตรียในปี ค.ศ. 1926
หากเปรียบเทียบกับฟิสิกส์แบบฉบับ
- กฎข้อที่สองของนิวตัน (F = ma) ใช้ทำนายการเคลื่อนที่ของวัตถุขนาดใหญ่ (เช่น รถยนต์, ลูกบอล) ว่าจะอยู่ที่ไหนเมื่อเวลาผ่านไป
- สมการชเรอดิงเงอร์ ใช้ทำนายพฤติกรรมของ อนุภาคขนาดเล็ก (เช่น อิเล็กตรอน, อะตอม) โดยบอกเราว่า “โอกาส” ที่จะพบอนุภาคในตำแหน่งต่าง ๆ เป็นอย่างไร
สมการชเรอดิงเงอร์เขียนในรูปแบบ ดังนี้:
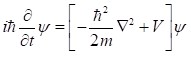

สรุปคือ สมการชเรอดิงเงอร์ แสดง
“อัตราการเปลี่ยนแปลงของฟังก์ชันคลื่นตามเวลา (ด้านซ้ายมือ) ซึ่งถูกกำหนดโดย พลังงานรวมของระบบ (ด้านขวามือ)”

การประยุกต์ใช้สมการชเรอดิงเงอร์ มีตัวอย่างสำคัญ ๆ ดังนี้:
- คำนวณโครงสร้างอะตอม: ใช้อธิบายว่าอิเล็กตรอนเคลื่อนที่รอบนิวเคลียสอย่างไร ทำให้เราเข้าใจตารางธาตุและปฏิกิริยาเคมี
- ปรากฏการณ์ลอดอุโมงค์ (Quantum Tunneling): อธิบายว่าอนุภาคสามารถทะลุผ่านกำแพงพลังงานที่ในทางฟิสิกส์แบบฉบับทำไม่ได้ได้อย่างไร
- การออกแบบวัสดุ: ใช้ทำนายสมบัติของวัสดุใหม่ ๆ เช่น การนำไฟฟ้า หรือความเป็นแม่เหล็กในระดับนาโน
การพัฒนาสมการชเรอดิงเงอร์นี้ถือเป็นการปฏิวัติวงการฟิสิกส์และเทคโนโลยีสมัยใหม่:
- รากฐานของเทคโนโลยีอิเล็กทรอนิกส์: ความเข้าใจพฤติกรรมของอิเล็กตรอนจากสมการนี้นำไปสู่การสร้าง สารกึ่งตัวนำ (Semiconductors), ทรานซิสเตอร์ และชิปคอมพิวเตอร์ที่เราใช้กันทุกวันนี้
- เลเซอร์ (Lasers): การเข้าใจระดับพลังงานของอะตอมทำให้เราสามารถสร้างแสงเลเซอร์ที่ใช้ในการแพทย์ การสื่อสาร และอุตสาหกรรม
- เคมีควอนตัม (Quantum Chemistry): ช่วยให้นักเคมีเข้าใจพันธะเคมีและการเกิดปฏิกิริยาได้อย่างลึกซึ้ง นำไปสู่การพัฒนายาและวัสดุสังเคราะห์ใหม่
- คอมพิวเตอร์ควอนตัม (Quantum Computing): หลักการเรื่อง Superposition (การซ้อนทับของสถานะ) ซึ่งอธิบายด้วยสมการชเรอดิงเงอร์ เป็นพื้นฐานสำคัญของการประมวลผลในคอมพิวเตอร์ควอนตัม
